Predicting Air Quality Exposures - Kriging

Because of a lack of air quality data collected at rural and remote locations, it has been necessary to use interpolation techniques to estimate O3 exposures in nonurban areas. In the absence of actual O3 data, interpolation techniques have been applied to the estimation of O3 exposures across the United States (Reagan, 1984; Lefohn et al., 1987; Knudsen and Lefohn, 1988). Kriging, a mathematical interpolation technique, has been used to provide estimates of seasonal O3 values for the National Crop Loss Assessment Network (NCLAN) for 1978 through 1982 (May-September for each year) (Reagan, 1984). These values, along with updated values, coupled with exposure-response models, were used to predict agriculturally related economic benefits anticipated by lower O3 levels in the United States (Adams et al., 1985; Adams et al., 1989).

Kriging is a statistical tool developed by Matheron (1963) and named in honor of D.G. Krige. Although originally developed specifically for ore reserve estimation, kriging has been used for other spatial estimation applications, such as analyzing and modeling air quality data (Grivet, 1980; Faith and Sheshenski, 1979). At its simplest, kriging can be thought of as a way to interpolate spatial data much as an automatic contouring program would. In a more precise manner, kriging can be defined as a best linear unbiased estimator of a spatial variable at a particular site or geographic area. Kriging assigns low weights to distant samples and vice versa, but also takes into account the relative position of the samples to each other and the site or area being estimated.

Because of the importance of the higher hourly average concentrations in eliciting injury and yield reduction for agricultural crops (U.S. EPA, 1986; 1992), Lefohn et al. (1992) used the W126 index (see Lefohn and Runeckles, 1987) and the number of hours greater than or equal to 100 ppb (N100) in its kriging to characterize the O3 exposures that occurred during the period 1985-1989. 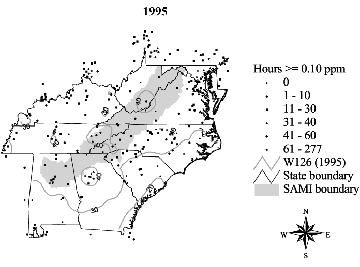Lefohn and co-workers used kriging, coupled with the Palmer Drought Index, to identify areas of concern for possible vegetation effects in the southern Appalachian mountains (Lefohn et al., 1997). The figure above illustrates the use of kriging to predict O3 exposures in the Southern Appalachian Mountains Initiative (SAMI) region. In September 1998, A.S.L. & Associates (Lefohn, 1998) completed a report identifying "Areas of Concern" for vegetation in the region.

An important question is: why not use only the W126 integrated exposure index instead of both the W126 and the N100 indices? The answer is that there are important concerns expressed in the literature with using the various cumulative exposure indices in predicting yield loss for agricultural crops or trees. For example, the same value of an exposure index may relate to different vegetation responses (Lefohn and Foley, 1992). Results reported by Yun and Laurence (1999) showed that the same SUM06 value resulted in very different foliar injury when exposure regimes with different numbers of high concentrations were applied. Similarly, Hogsett et al. (1985) showed that the same SUM07 value resulted in different yield when exposure regimes, some containing peaks and some without peaks, were used. Lefohn and Foley (1992) proposed an approach to get around the problem. They combined the W126 cumulative exposure index with the N100 index. The N100 index was selected because the original experimental NCLAN data used to determine the exposure-response relationships contained numerous occurrences of hourly average concentrations greater than or equal to 100 ppb. Recently, Davis and Orendovici (2006) reported that they had successfully developed a model that showed a statistically significant relationship between indices of ozone symptoms and the following parameters: plant species, Palmer Drought Severity Index, and the interaction of the W126 exposure index and the N100 index. The authors reported that the incidence of ozone symptoms was most related to the ozone metrics W126 index coupled to the N100 index.

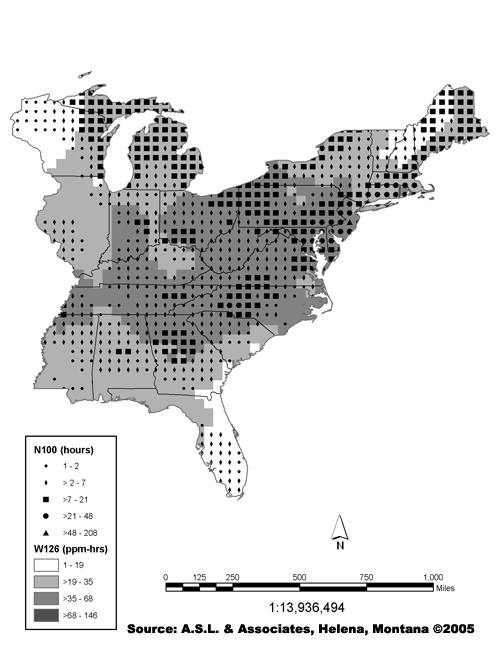
In 2003, Lefohn and co-workers used kriging to characterize the number of hours greater than or equal to 100 ppb (N100) and the W126 exposures for 2001 in the United States. The figure below illustrates the N100 and 24-hour W126 values for the summer of 2001.

A brief discussion follows on why ordinary kriging was selected for the analysis above rather than another method.

Indicator kriging is used when it is desired to estimate a distribution of values within an area rather than just the mean value of an area. As the purpose of the study was to estimate the mean values of the N100 and W126 exposure indices within an area rather than the distribution of values, Indicator Kriging was not selected.

Universal Kriging was not chosen for this study for several reasons. Universal kriging is used to estimate spatial means when the data have a strong trend and the trend can be modeled by simple functions. Trend is scale dependent. For example The University of Montana Tech sits on the south side of a hill high above the valley Butte, Montana is located in. A model of the elevations around Montana Tech would show that a trend in the values exists when you look north. If you want to model the elevation to the north of Montana Tech, it can be accurately done with a simple straight line. At the scale of 1/4 mile the local data has a trend. This trend does not exist for far however. If you continue north for say 60 miles, you encounter Helena, Montana. Along the way the elevation rises and falls many times as you cross mountains and valleys. On the scale of 60 miles, there is no trend in the elevation. Ozone data may display trends over small geographic areas but at the scale of the entire United States, there is no trend that can be modeled by simple functions.

Co-kriging is an extension of kriging used when estimating a one variable from two variables. The two co-variables must have a strong relationship and this relationship must be defined. Use of Co-Kriging requires the spatial covariance model of each variable and the cross-covariance model of the variables. The method can be quite difficult to do because developing the cross-covariance model is quite complicated. Developing the relationship between the two variables can also be complicated. Practice in the mining industry limits Co-Kriging to the case when the variable being estimated is under sampled with respect to the second variable. If all samples have both variables, industry has found no benefit gained from the use of Co-Kriging.

Co-Kriging was not chosen for this study because the O3 indices N100 and W126 are sampled at each location. Also, there has been no study that has identified a secondary variable from more sampling sites that is highly correlated to these exposure indices that can be used to predict these indices.

Ordinary kriging was selected for this study based on how well it has performed on prior years data and because the statistical characteristics of the data in 2000 and 2003 make Ordinary Kriging the appropriate choice of estimator. The data displayed no trend at the scale of the modeling; thus universal kriging was not appropriate. The covariance models (variogram) exhibited local stationary and thus, Ordinary Kriging was the appropriate technique to use.

Our research team has used ordinary kriging to make ground-level O3 models for the years from 1982 to 2003. While the O3 values vary from year to year, the statistical character of the data remains remarkably constant from year to year. The covariance models are similar in each year and the spatial anisotropy exhibited by the co-variance models is similar in each year. If you have a need for our technical expertise, please email us. We would be pleased to discuss how your specific needs may match with our capabilities to integrate spatial variability quantification with unique mapping presentations.

It has been stated that kriging has its shortcomings. In particular, the current version of the EPA's Criteria Document (2006) states that kriging variance underestimates the uncertainty in spatial prediction and relies on the assumption of spatial covariance isotropy. Kriging does not require an isotropic covariance model. For example, the spatial covariance model used in our study was anisotropic. If the spatial covariance were underestimated or there were an additional source of variation that was not accounted for in the model (e.g., temporal variation), then the kriging variance could be underestimated. However, in our kriging effort, we did not construct a model that modeled the temporal variation because seasonal cumulative data were selected for the study. Also, in many of our current studies, instead of using the Ordinary Kriging variance, we use the Ordinary Interpolation variance developed by Yamamoto (2005). Yamamoto derived an error variance for Ordinary kriging that is conditional to the data values. He has shown that the Ordinary interpolation variance is a better measure of accuracy of the kriging estimate. In our current efforts, the Ordinary kriging programs used are modified to calculate the new error variance. We believe that the new method used in our study to determine the interpolation variance is a better estimate of the error variance than the kriging variance. In particular, for skewed data, it is believed that the new variance is a much better estimate of the error variance.

References

Adams, R.M.; Hamilton, S.A.; McCarl, B.A. (1985) An assessment of the economic effects of ozone on U.S. agriculture. J. Air Pollut. Control Assoc. 35:938-943.

Adams, R.M.; Glyer, J.D.; Johnson, S.L.; McCarl, B.A. (1989) A reassessment of the economic effects of ozone on U.S. agriculture. J. Air Pollut. Control Assoc. 39:960-968.

Davis, D.D.; Orendovici, T. (2006). Incidence of ozone symptoms on vegetation within a National Wildlife Refuge in New Jersey, USA. Environ. Pollut. 143:555-564.

Faith, R.; Sheshinski, R. (1979) Misspecification of trend in spatial random-function interpolation with application to oxidant mapping. Palo Alto, California: SIAM Institute for Mathematics and Society, Stanford University; Technical Report No. 28.

Grivet, C.D. (1980) Modeling and analysis of air quality data. Palo Alto, California: SIAM Institute for Mathematics and Society, Stanford University; Technical Report No. 43.

Hogsett, W. E.; Tingey, D. T.; Holman, S. R. (1985) A programmable exposure control system for determination of the effects of pollutant exposure regimes on plant growth. Atmos. Environ. 19: 1135-1145.

Knudsen, H.P.; Lefohn, A.S. (1988) The use of geostatistics to characterize regional ozone exposures. In: Heck, W.W.; Taylor, O.C.; Tingey, D.T.. eds. Assessment of crop loss from air pollutants. London, U.K.: Elsevier Science Publishers, LTD; pp. 91-105.

Lefohn, A.S. (1998) The identification of ozone exposures that result in vegetation injury and growth loss for specific species grown in the Southern Appalachian Mountain region. Prepared for the Southern Appalachian Mountains Initiative, Asheville, North Carolina. September 1998.

Lefohn, A. S.; Foley, J. K. (1992) NCLAN results and their application to the standard-setting process: protecting vegetation from surface ozone exposures. J. Air Waste Manage. Assoc. 42: 1046-1052.

Lefohn, A.S.; Runeckles, V.C. (1987) Establishing a standard to protect vegetation - ozone exposure/dose considerations. Atmos. Environ. 21:561-568.

Lefohn, A.S.; Jackson, W.; Shadwick, D.S.; Knudsen, H.P. (1997) Effect of Surface Ozone Exposures on Vegetation Grown in the Southern Appalachian Mountains: Identification of Possible Areas of Concern. Atmos. Environ. 31(11):1695-1708.

Lefohn, A.S.; Knudsen, H.P.; Logan, J.A.; Simpson, J.; Bhumralkar, C. (1987) An evaluation of the kriging method to predict 7-h seasonal mean ozone concentrations for estimating crop losses. J. Air Pollut. Control Assoc. 37:595-602.

Lefohn, A.S.; Knudsen, H.P.; Shadwick, D.S.; Hermann, K.A. (1992) Surface ozone exposures in the eastern United States (1985-1989). In: Flagler, R.B., ed. Transactions of the response of southern commercial forests to air pollution specialty conference. Pittsburgh, PA: Air & Waste Management Association; pp. 81-93.

Matheron, G. (1963) Principles of geostatistics. Economic Geol. 58:1246-1266.

Reagan, J. (1984) Air quality interpretation. In: National Crop Loss Assessment Network (NCLAN) 1982 annual report. Corvallis, OR: U.S. Environmental Protection Agency; EPA-600/3-84-049, pp. 198-219.

U.S. Environmental Protection Agency (1986) Air quality criteria for ozone and other photochemical oxidants, Vol. V. Research Triangle Park, NC; Office of Environmental Criteria and Assessment; EPA report no. EPA/600/8-84/020ef. Available from: NTIS, Springfield, VA.

U.S. Environmental Protection Agency (1992) Summary of selected new information on effects of ozone on health and vegetation: Draft supplement to air quality criteria for ozone and other photochemical oxidants. Washington, DC.: U.S. Environmental Protection Agency, Office of Health and Environmental Assessment; EPA report no. EPA-600/8-88/105A. Available from: NTIS, Springfield, VA.

U.S. Environmental Protection Agency (2006) Air Quality Criteria for Ozone and Related Photochemical Oxidants. Research Triangle Park, NC: Office of Research and Development; report no. EPA/600/R-05/004af.

Yamamoto, J.K. (2005) Comparing ordinary kriging interpolation variance and indicator kriging conditional variance for assessing uncertainties at unsampled locations, In: Application of Computers and Operations Research in the Mineral Industry - Dessureault, Ganguli, Kecojevic,& Dwyer editors, Balkema.

Yun, S-C.; Laurence, J.A. (1999) The response of sensitive and tolerant clones of Populus tremuloides to dynamic ozone exposure under controlled environmental conditions. New Phytologist 143: 305-313.